Page 57 - 169

де:
 1  n  (K  ) 1 - кількість степенів свободи моделі;
K - кількість параметрів моделі.
Аналогічно знаходять величину дисперсії, що характеризує похибки
вимірювання вихідної величини:
S
S 2  D
D

2
де:
 2  n ( v ) 1 .
Відношення дисперсії, що характеризує точність реалізації моделі та
дисперсії, що характеризує похибки вимірювання вихідної величини
визначають адекватність моделі.

S 2
F  e .
S 2
D
Якщо:
F→ 1 - то модель буде адекватною;
F→ ∞ - то модель не адекватна.
Для формалізації цього правила використовують розподілення Фішера,
яке залежить від величин (φ 1) і (φ 2). Якщо прийняти, що степінь надійності
перевірки гіпотези (α) то на основі (φ 1) і (φ 2) визначають максимально
допустиме значення (F кр) для забезпечення необхідної адекватності моделі.
Якщо:
F<F кр - то гіпотеза про адекватність моделі буде вірною;
F>F кр - то гіпотеза про адекватність моделі не приймається.

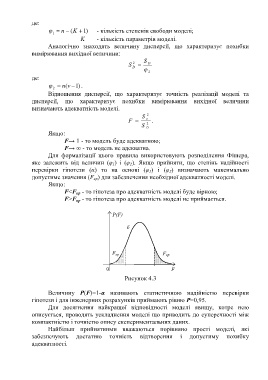
P(F)

б

F кр F кр

0 F

Рисунок 4.3

Величину P(F)=1-α називають статистичною надійністю перевірки
гіпотези і для інженерних розрахунків приймають рівню P=0,95.
Для досягнення найкращої відповідності моделі явищу, котре нею
описується, проводять ускладнення моделі що приводить до суперечності між
компактністю і точністю опису експериментальних даних.
Найбільш прийнятними вважаються порівняно прості моделі, які
забезпечують достатню точність відтворення і допустиму похибку
адекватності.