Page 175 - 157

Обрахунки проведемо в наступній послідовності:
1) Визначаємо центральні і початкові моменти
2
 m x 1295  m  x 3023
x  a  i i   . 1 1816; a  i i   . 2 76;
2
1
 m i 1096  m i 1096
3
 m  x 90305
a  i i   82 4 . .
3
 m i 1096
2
m  a  a  . 1 362;
2
2
1
3
m  a  a 3 1 a  a 2 1  . 0 116.
3
2
3
Для закону Пуассона a  m  m . В даному випадку m 3 значно
1
3
2
відрізняється від а 1 і m 2. Тому необхідно вичислити поправку Шарльє. Якщо
вводиться поправка Шарльє, то моменти m 2 i m 3 в розрахунках не
використовуються. Тому в тих випадках, коли необхідність поправки Шарльє
очевидна заздалегідь, обраховувати m 2 i m 3 не слід.
x
2) Для x  a  2 . 1 знаходимо P  P   і заповнюємо колонку 6.
m n , i
3) Перемноживши значення Р(х і) на N = 1096, отримаємо значення
частот, вирівнювання по закону Пуассона (колонка 7).
4) Підставивши значення S і x в (а) і зробивши перетворення, отримаємо
m   m  0646.0 x x  1  0 . 1527 x  . 0 0902  A .
 m 
i i i i i i 3
Після обрахунку значення А заповнюємо колонку 8.
5) В колонці 9 дані добутки m A .
i i
6) В колонці 10 дані m   i m  m  .

i
i
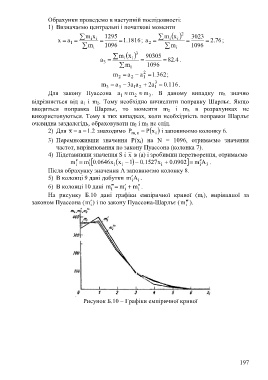
На рисунку Б.10 дані графіки емпіричної кривої (m i), вирівняної за
законом Пуассона (m) і по закону Пуассона-Шарльє (m  ).
i
i

Рисунок Б.10 – Графіки емпіричної кривої

197