Page 145 - 157

Приклад 8.1.

Нехай необхідно виявити наявність кореляційного зв’язку між розмірами
моделей і відливок до них. Шляхом вимірювання окремих відхилень від
номіналів висот моделей для 11 моделей (х і) і відливок (у і). Послідовність
обрахунку зрозуміла із таблиці 8.3.

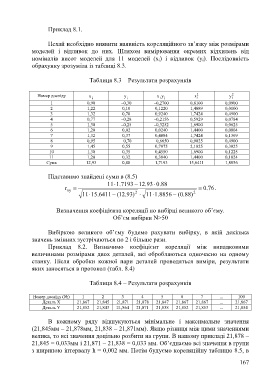
Таблиця 8.3 – Результати розрахунків

2
2
Номер досліду x y x y x y
i i i i i i
1 0,90 –0,30 –0,2700 0,8100 0,0900
2 1,22 0,10 0,1220 1,4889 0,0100
3 1,32 0,70 0,9240 1,7424 0,4900
4 0,77 –0,28 –0,2156 0,5929 0,0784
5 1,30 –0,25 –0,3252 1,6900 0,0625
6 1,20 0,02 0,0240 1,4400 0,0004
7 1,32 0,37 0,4884 1,7424 0,1369
8 0,95 –0,70 –0,6650 0,9025 0,4900
9 1,45 0,55 0,7975 2,1025 0,3025
10 1,30 0,35 0,4550 1,6900 0,1225
11 1,20 0,32 0,3840 1,4400 0,1024
Сума 12,93 0,88 1,7193 15,6411 1,8856

Підставимо знайдені суми в (8.5)
11 . 1 7193  12 . 93 . 0  88
r   . 0 76.
xy
2
11 15 . 6411 ( 12 . 93 )  11 . 1 8856  . 0 ( 88 ) 2

Визначення коефіцієнта кореляції по вибірці великого об’єму.
Об’єм вибірки N>50

Вибіркою великого об’єму будемо рахувати вибірку, в якій декілька
значень змінних зустрічаються по 2 і більше рази.
Приклад 8.2. Визначимо коефіцієнт кореляції між випадковими
величинами розмірами двох деталей, які обробляються одночасно на одному
станку. Після обробки кожної пари деталей проводяться виміри, результати
яких заносяться в протокол (табл. 8.4)

Таблиця 8.4 – Результати розрахунків

Номер досліду (№) 1 2 3 4 5 6 7 ... 100
Деталь Х 21,867 21,845 21,871 21,878 21,847 21,867 21,867 ... 21,867
Деталь Y 21,852 21,843 21,864 21,871 21,838 21,852 21,853 ... 21,854

В кожному ряду відшукуються мінімальне і максимальне значення
(21,845мм – 21,878мм, 21,838 – 21,871мм). Якщо різниця між цими значеннями
велика, то всі значення доцільно розбити на групи. В нашому прикладі 21,878 –
21,845 = 0,033мм і 21,871 – 21,838 = 0,033 мм. Об’єднаємо всі значення в групи
з шириною інтервалу h = 0,002 мм. Потім будуємо кореляційну таблицю 8.5, в

167