Page 70 - Лекція 6

Очевидно, що (6.3) є загальною формулою для всіх
розглянутих умов.
Нехай дві функції f(x) i g(x) визначені та непе-рервні на
[a,b] і такі, що f x( ) g x( )для всіх x [a,b]. Фігура, обмежена
графіками цих функцій і , можливо відрізками прямих х=a й
х=b, ординати точок яких змінюються відповідно від g(a) до
f(a) та від g(b) до f(b), називається криволінійною трапецією,
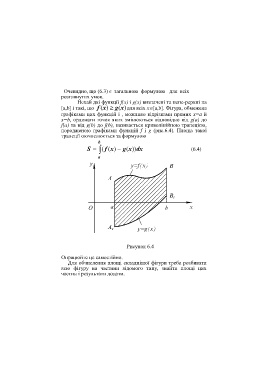
породженою графіками функцій f i g (рис.6.4). Площа такої
трапеції оючислюється за формулою
b
S ( f x( ) g x dx( )) (6.4)

a

Рисунок 6.4

Опрацюйте це самостійно.
Для обчислення площі складнішої фігури треба розбивати
всю фігуру на частини відомого типу, знайти площі цих
частин і результати додати.