Page 68 - Лекція 6

Лекція 6
Застосування визначеного інтеграла.

Перший клас задач, для розв’язання яких вико-
ристовується визначений інтеграл, пов’язаний з обчис-ленням
певних величин (площі фігури, довжини дуги кривої, роботи,
яка виконується певною силою та інші). В таких задачах
метод обчислення пов’язаний з означенням такої величини.
До другого класу (їх розглянемо пізніше) нале-жать
задачі, в яких спочатку складають відповідне співвідношення
(диференціальне рівняння, його розв’язком є функція ), а
потім переходять за допомогою інтегрування до відповідного
співвідношення між змінними.

6.1. Геометричні застосування інтеграла.

1. Обчислення площ плоских фігур.
а) Випадок прямокутних координат.
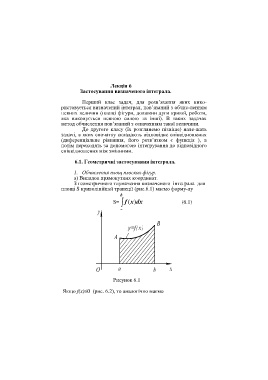
З геометричного тлумачення визначеного інтеграла для
площі S криволінійної трапеції (рис.6.1) маємо форму-лу
b
S= f x dx( ) (6.1)
a

Рисунок 6.1

Якщо f(x) 0 (рис. 6.2), то аналогічно маємо