Page 19 - Міністерство освіти і науки України

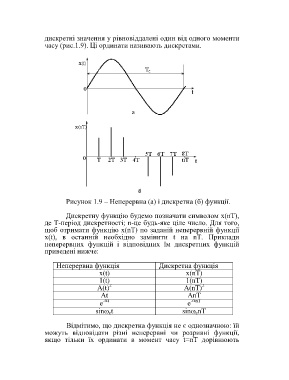
дискретні значення у рівновіддалені один від одного моменти
часу (рис.1.9). Ці ординати називають дискретами.

Рисунок 1.9 – Неперервна (а) і дискретна (б) функції.

Дискретну функцію будемо позначати символом x(nT),
де T-період дискретності; n-це будь-яке ціле число. Для того,
щоб отримати функцію x(nT) по заданій неперервній функції
x(t), в останній необхідно замінити t на nT. Приклади
неперервних функцій і відповідних їм дискретних функцій
приведені нижче:

Неперервна функція Дискретна функція
x(t) x(nT)
1(t) 1(nT)
2
2
A(t) A(nT)
At AnT
- t
e e - nT
sin t sin nT
c
c

Відмітимо, що дискретна функція не є однозначною: їй
можуть відповідати різні неперервні чи розривні функції,
якщо тільки їх ординати в момент часу t=nT дорівнюють