Page 237 - 70

Відносна похибка вимірювальної схеми досліджуваної струк-
тури засобу вимірювання буде такою:
s  s   s  1 s  s s s 
  1  2 3  4  4 5 4 .
s 1 s  s 3 1 s 4 s 5 s 4 1 s 4 s 5 s 5
2

6.5. Похибки засобів вимірювань внаслідок нелінійності їх
статичних характеристик

У деяких вимірювальних приладах статична характеристика є
нелінійною. Нелінійність може бути викликана фізичним принци-
пом перетворення вимірюваної фізичної величини, застосуванням
матеріалів з різними фізичними властивостями або зміною техноло-
гії виготовлення приладу тощо. На рис. 6.5 наведено дві статичні
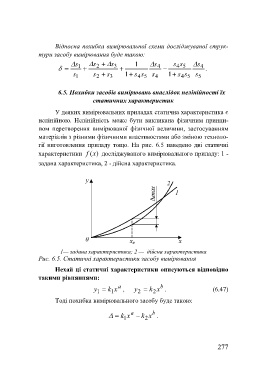
характеристики (xf ) досліджуваного вимірювального приладу: 1 -
задана характеристика, 2 - дійсна характеристика.

1— задана характеристика; 2 — дійсна характеристика
Рис. 6.5. Статичні характеристики засобу вимірювання
Нехай ці статичні характеристики описуються відповідно
такими рівняннями:
a b
y  k 1 x , y  k 2 x . (6.47)
2
1
Тоді похибка вимірювального засобу буде такою:
a b
  k 1 x  k 2 x .

277