Page 251 - 68

Додатки

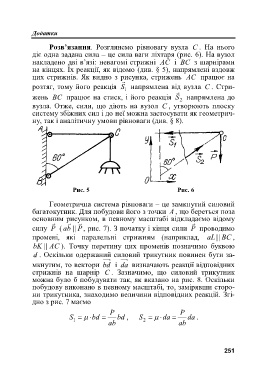
Розв’язання. Розглянемо рівновагу вузла C . На нього
діє одна задана сила – це сила ваги ліхтаря (рис. 6). На вузол
накладено дві в’язі: невагомі стрижні AC і BC з шарнірами
на кінцях. Їх реакції, як відомо (див. § 5), напрямлені вздовж
цих стрижнів. Як видно з рисунка, стрижень AC працює на

розтяг, тому його реакція S напрямлена від вузла C . Стри-
1

жень BC працює на стиск, і його реакція S напрямлена до
2
вузла. Отже, сили, що діють на вузол C , утворюють плоску
систему збіжних сил і до неї можна застосувати як геометрич-
ну, так і аналітичну умови рівноваги (див. § 8).

Рис. 5 Рис. 6

Геометрична система рівноваги – це замкнутий силовий
багатокутник. Для побудови його з точки A , що береться поза
основним рисунком, в певному масштабі відкладаємо відому




силу P ( ba || P , рис. 7). З початку і кінця сили P проводимо
промені, які паралельні стрижням (наприклад, aL || BC ,
bK || AC ). Точку перетину цих променів позначимо буквою
d . Оскільки одержаний силовий трикутник повинен бути за-
мкнутим, то вектори bd і da визначають реакції відповідних
стрижнів на шарнір C . Зазначимо, що силовий трикутник
можна було б побудувати так, як вказано на рис. 8. Оскільки
побудову виконано в певному масштабі, то, замірявши сторо-
ни трикутника, знаходимо величини відповідних реакцій. Згі-
дно з рис. 7 маємо
P P
S    bd  bd , S    da  da .
1
2
ab ab

251