Page 96 - 6792

Функція розподілу Вейбула:
 t  

F   t 1 e  , (3.9)
де β – параметр форми, η – параметр масштабу,  – параметр
зміщення.
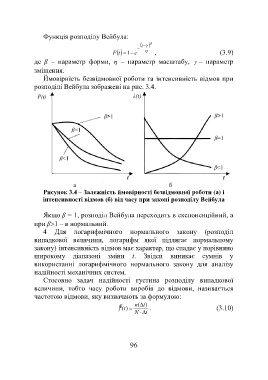
Ймовірність безвідмовної роботи та інтенсивність відмов при
розподілі Вейбула зображені на рис. 3.4.

Рисунок 3.4 – Залежність ймовірності безвідмовної роботи (а) і
інтенсивності відмов (б) від часу при законі розподілу Вейбула

Якщо β = 1, розподіл Вейбула переходить в експоненційний, а
при β1 – в нормальний.
4 Для логарифмічного нормального закону (розподіл
випадкової величини, логарифм якої підлягає нормальному
закону) інтенсивність відмов має характер, що спадає у порівняно
широкому діапазоні зміни t. Звідси виникає сумнів у
використанні логарифмічного нормального закону для аналізу
надійності механічних систем.
Стосовно задач надійності густина розподілу випадкової
величини, тобто часу роботи виробів до відмови, називається
частотою відмови, яку визначають за формулою:
€
f ( t ) n( t  ) . (3.10)
N  t 

96