Page 41 - 6505

Пряма y=3t-5 перетинає логарифмічну криву в двох точках з

абсцисами ≈ 0,00001 і ≈ 1,75. На рисунку важко показати

перетин графіків цих двох функцій в першій точці, але,
враховуючи, що нижня вітка логарифмічної кривої необмежено

прямує до осі Оу, можливо уявити, що перетин цих двох графіків
пройде поблизу точки перетину графіка функції y=3t-5 і осі Оу.

Абсциса точки перетину наближено дорівнює 0,00001. Отже
корені рівняння ≈ 0,00001 і ≈ 1,75.

Аналітичний метод. Аналітично корені рівняння f(t)=0

можна відокремити, використовуючи деякі властивості функцій та
одну з розглянутих нижче теорем.

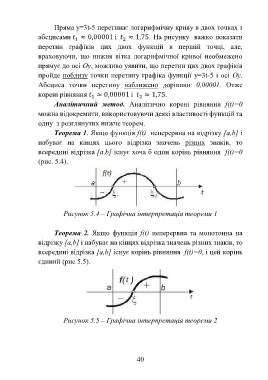
Теорема 1. Якщо функція f(t) неперервна на відрізку [a,b] і

набуває на кінцях цього відрізка значень різних знаків, то
всередині відрізка [a,b] існує хоча б один корінь рівняння f(t)=0

(рис. 5.4).

Рисунок 5.4 – Графічна інтерпретація теореми 1

Теорема 2. Якщо функція f(t) неперервна та монотонна на
відрізку [a,b] і набуває на кінцях відрізка значень різних знаків, то

всередині відрізка [a,b] існує корінь рівняння f(t)=0, і цей корінь

єдиний (рис 5.5).

Рисунок 5.5 – Графічна інтерпретація теореми 2

40