Page 12 - 6449

Рисунок 1.4 – ОДР – замкнута випукла множина

З рис. 1.1-1.4 видно, що фактично ОДР – це та частина першої
координатної чверті, в якій перетинаються всі зони штриховки. Отже, ОДР
– це шестикутник. В даному випадку ЗЛП може мати один або безліч
розв’язків.
Г. Необмежена випукла множина

х 1  4х 2  4
Якщо система обмежень (1.10) має вигляд: 
 4х 1  х 2  ,4
то ОДР набуває вигляду необмеженої випуклої множини, яка подана на
рис.1.5.

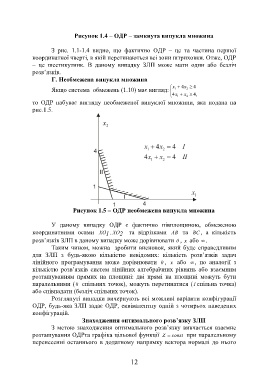
Рисунок 1.5 – ОДР необмежена випукла множина

У даному випадку ОДР є фактично півплощиною, обмеженою
координатними осями XO 1 , XO 2 та відрізками AB та BC , а кількість
розв’язків ЗЛП в даному випадку може дорівнювати 0 , x або .
Таким чином, можна зробити висновок, який буде справедливим
для ЗЛП з будь-якою кількістю невідомих: кількість розв’язків задач
лінійного програмування може дорівнювати 0 , x або , по аналогії з
кількістю розв’язків систем лінійних алгебраїчних рівнянь або взаємним
розташуванням прямих на площині: дві прямі на площині можуть бути
паралельними (0 спільних точок), можуть перетинатися (1спільна точка)
або співпадати (безліч спільних точок).
Розглянуті випадки вичерпують всі можливі варіанти конфігурації
ОДР, будь-яка ЗЛП задає ОДР, еквівалентну одній з чотирьох наведених
конфігурацій.
Знаходження оптимального розв’язку ЗЛП
З метою знаходження оптимального розв’язку вивчається взаємне
розташування ОДРта графіка цільової функції Z  const при паралельному
перенесенні останнього в додатному напрямку вектора нормалі до нього

12