Page 35 - 6374

часу ∆ швидкість змінилася на ∆ = + ∆ − . Середнє прискорення за час ∆

дорівнює:

∆
, + ∆ = (13)
∆

Зображатимемо вектори у будь-які моменти часу такими, які виходять з спільного
початку. Кінець вектора опише криву, яка називається годографом швидкостей.

Зменшуючи необмежено проміжок часу ∆, на якому визначається середня швидкість,

отримаємо у границі прискорення:

∆
= lim = . (14)
∆→0 ∆

Оскільки = , а = + + , то прискорення можна виразити у вигляді

2

= , або
2

2
2
2

= + + . (15)
2 2 2

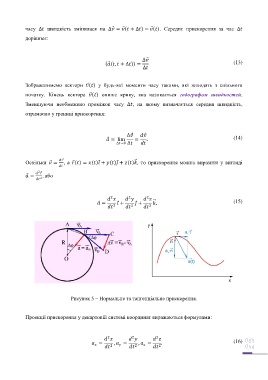
Рисунок 5 – Нормальне та тангенціальне прискорення.

Проекції прискорення у декартовій системі координат виражаються формулами:

2
2
2

= , = , = . (16)

2 2 2