Page 14 - 6028

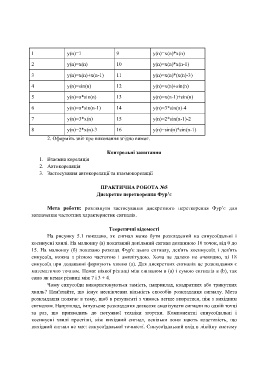
1 y(n)=1 9 y(n)=x(n)*x(n)

2 y(n)=x(n) 10 y(n)=x(n)*x(n-1)

3 y(n)=x(n)+x(n-1) 11 y(n)=x(n)*(x(n)-3)

4 y(n)=sin(n) 12 y(n)=x(n)+sin(n)

5 y(n)=n*sin(n) 13 y(n)=x(n-1)+sin(n)

6 y(n)=n*sin(n-1) 14 y(n)=3*sin(n)-4

7 y(n)=3*x(n) 15 y(n)=2*sin(n-1)-2

8 y(n)=2*x(n)-3 16 y(n)=sin(n)*sin(n-1)

2. Оформіть звіт про виконання згідно вимог.

Контрольні запитання
1. Взаємна кореляція
2. Автокореляція
3. Застосування автокореляції та взаємокореляції

ПРАКТИЧНА РОБОТА №5
Дискретне перетворення Фур’є

Мета роботи: розглянути застосування дискретного перетворення Фур’є для
визначення частотних характеристик сигналів.

Теоретичні відомості
На рисунку 5.1 показано, як сигнал може бути розкладений на синусоїдальні і
косинусні хвилі. На малюнку (а) показаний довільний сигнал довжиною 16 точок, від 0 до
15. На малюнку (б) показано розклад Фур'є цього сигналу, дев'ять косинусоїд і дев'ять
синусоїд, кожна з різною частотою і амплітудою. Хоча це далеко не очевидно, ці 18
синусоїд при додаванні формують хвилю (а). Для дискретних сигналів це розкладання є
математично точним. Немає ніякої різниці між сигналом в (a) і сумою сигналів в (b), так
само як немає різниці між 7 і 3 + 4.
Чому синусоїди використовуються замість, наприклад, квадратних або трикутних
хвиль? Пам'ятайте, що існує нескінченна кількість способів розкладання сигналу. Мета
розкладання полягає в тому, щоб в результаті з чимось легше впоратися, ніж з вихідним
сигналом. Наприклад, імпульсне розкладання дозволяє аналізувати сигнали по одній точці
за раз, що призводить до потужної техніки згортки. Компонентні синусоїдальні і
косинусні хвилі простіші, ніж вихідний сигнал, оскільки вони мають властивість, що
вихідний сигнал не має: синусоїдальної точності. Синусоїдальний вхід в лінійну систему