Page 124 - 480

фіксувати зміну осьового навантаження F на долото в дискретні
i
моменти часу t .
i

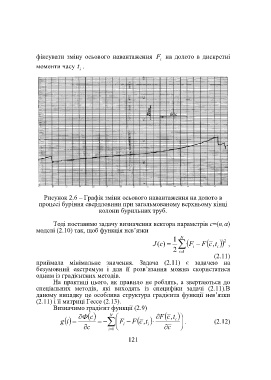
Рисунок 2.6 – Графік зміни осьового навантаження на долото в
процесі буріння свердловини при загальмованому верхньому кінці
колони бурильних труб.

Тоді поставимо задачу визначення вектора параметрів с=(n,)
моделі (2.10) так, щоб функція нев’язки
1 N 2
J( c)   F i  F  tc, i  ,
2  i 1
(2.11)
приймала мінімальне значення. Задача (2.11) є задачею на
безумовний екстремум і для її розв’язання можна скористатися
одним із градієнтних методів.
На практиці цього, як правило не роблять, а звертаються до
спеціальних методів, які виходять із специфіки задачі (2.11).В
даному випадку це особлива структура градієнта функції нев’язки
(2.11) і її матриці Гессе (2.13).
Визначимо градієнт функції (2.9)
Ф  с N  F  tc, 
g   i     F i  F  tc, i  i  . (2.12)
с i 1 c 
 
121