Page 45 - 4757

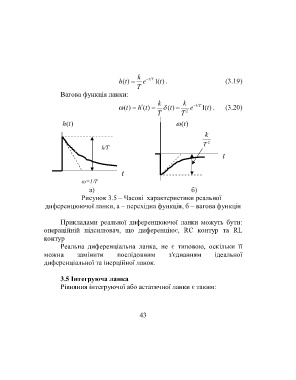
k  / t T
h ( )t  e 1( )t . (3.19)
T
Вагова функція ланки:
k k
 ( )t  h ( )t   ( )t  e  / t T 1( )t . (3.20)
T T 2
h ( )t  ( )t
k

T 2
k/T
t

t
ω=1/T
а) б)
Рисунок 3.5 – Часові характеристики реальної
диференцюючої ланки, а – перехідна функція, б – вагова функція

Прикладами реальної диференцюючої ланки можуть бути:
операційній підсилювач, що диференціює, RC контур та RL
контур
Реальна диференціальна ланка, не є типовою, оскільки її
можна замінити послідовним з'єднанням ідеальної
диференціальної та інерційної ланок.

3.5 Інтегруюча ланка
Рівняння інтегруючої або астатичної ланки є таким:

43