Page 45 - 4660

Important discrete distributions

p = 0.4, r = 2

0.15
p = 0.4, r = 4
0.10
0.10
0.08
0.05 0.06
0.04
0 2 4 6 8 10 0 2 4 6 8 10
p = 0.8, r = 4

0.40

0.30

0.20
p = 0.8, r = 12
0.20
0.15
0.10
0.10
0.05
0.00
0 2 4 6 8 10 0 2 4 6 8 10
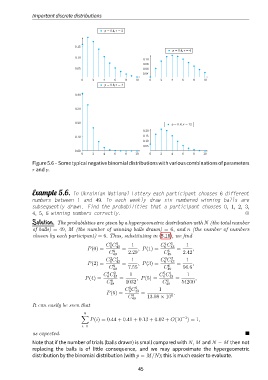
Figure 5.6 – Some typical negative binomial distributions with various combinations of parameters
r and p.

Example 5.6. In Ukrainian National Lottery each participant chooses 6 different
numbers between 1 and 49. In each weekly draw six numbered winning balls are
subsequently drawn. Find the probabilities that a participant chooses 0, 1, 2, 3,
4, 5, 6 winning numbers correctly. ,

Solution. The probabilities are given by a hypergeometric distribution with N (the total number
of balls) = 49, M (the number of winning balls drawn) = 6, and n (the number of numbers
chosen by each participant) = 6. Thus, substituting in (5.16), we find
0
1
C C 6 1 C C 5 1
P(0) = 6 43 = , P(1) = 6 43 = ,
6
5
C 49 2.29 C 49 2.42
2
3
C C 4 1 C C 3 1
P(2) = 6 43 = , P(3) = 6 43 = ,
C 6 7.55 C 6 56.6
49 49
5
4
C C 2 1 C C 1 1
P(4) = 6 43 = , P(5) = 6 43 = ,
6
6
C 49 1032 C 49 54200
6
C C 0 1
P(6) = 6 43 = .
6
C 49 13.98 × 10 6
It can easily be seen that
6
∑ −3
P(i) = 0.44 + 0.41 + 0.13 + 0.02 + O(10 ) = 1,
i=0
as expected.
Note that if the number of trials (balls drawn) is small compared with N, M and N − M then not
replacing the balls is of little consequence, and we may approximate the hypergeometric
distribution by the binomial distribution (with p = M/N); this is much easier to evaluate.
45