Page 125 - 4617

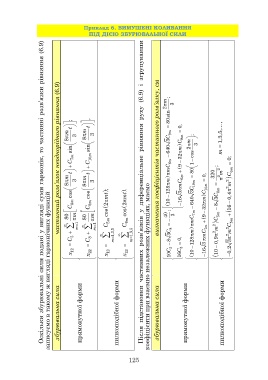
Приклад 6. ВИМУШЕНІ КОЛИВАННЯ
ПІД ДІЄЮ ЗБУРЮВАЛЬНОЇ СИЛИ

згрупувавши
Оскільки збурювальні сили подані у вигляді суми гармонік, то частинні розв’язки рівняння (6.9)

частинний розв’язок неоднорідного рівняння (6.9)
і
(6.9) m ;

руху 2 3

80sin
,
; 0,
рівняння 3C C 9m 2 3 
3    3   9m  ; 1,3,5,...,
m t 
m t 

7m sin    sin   10m  визначення коефіцієнтів частинного розв’язку, см 640 m m  cos   m 0;
C 8    8  C   mC  6m 9 32  1 ; 2  6m

3   m t   3  диференціальне   m  mC 6m  80   10m  0,  320 2 m  2 2 m C
m t 
; . 3C C 10m  6m
записуємо в такому ж вигляді гармонічних функцій
mt mt 128 3 3C
6m cos   cos   9m 2 2 10  16 640 m 0,4
C 8 8 C у       32 8 16 




80 m  80 m  cos 5m cos 6m 40 ; 3 mC  7m 9   5m  5m
  1 m   1 m C C розв’язків  8  7m 2 mC 2  2 mC 2
  1,3,5   1,3,5 3C    m mC
5 8
C C m m 8 0,
  5  8 128 3  0,9 3
частинних коефіцієнти при взаємно незалежних функціях, маємо  
12 22 12 22 16 0,2
x     x   x x 10C  16C 10  10 
                            

збурювальна сила прямокутної форми пилкоподібної форми підстановки збурювальна сила прямокутної форми пилкоподібної форми







Після
125