Page 88 - 4570
P. 88
87
Означення 2.47. Дефазифікацією (в нечіткій логіці) називається
процедура перетворення нечіткої множини в чітке число.
У теорії нечітких множин процедура дефаззіфікації аналогічна
знаходженню характеристик стану (математичного сподівання, моди, медіани)
випадкових величин у теорії ймовірності. Наприклад, таким числом може стати
максимум функції належності, центр ваги функції належності і т. д.
2. Операції над нечіткими множинами
Визначення нечітких теоретико-множинних операцій можуть бути
узагальнені із теорії звичайних множин.
Означення 2.48. Дві нечіткі множини A і B , що задані на U, є рівними,
якщо вони складаються з одних і тих самих елементів для всіх x U та A(x) =
B (x). Позначають як A = B .
Означення 2.49. Дві нечіткі множини A і B доповнюють одна одну,
якщо A(x) = 1 - B(x) для всіх x U.
Означення 2.50. Перетином двох нечітких множин A і B є така
множина D = A B , що складається з елементів для всіх x U, що
одночасно належать A і B із функцією належності D(x) = min( A(x), B (x)).
Означення 2.51. Об’єднанням двох нечітких множин A і B є така
множина D = A B , що складається із елементів для всіх x U, що
належать A або B з функцією належності D(x)= max( A(x), B (x)).
Означення 2.52. Різницею двох нечітких множин A і B є така множина
D = A - B , що складається з елементів для всіх x U, що мають функцію
належності D(x) = A(x) - B (x), якщо A(x) > B (x)), інакше D(x) = 0.
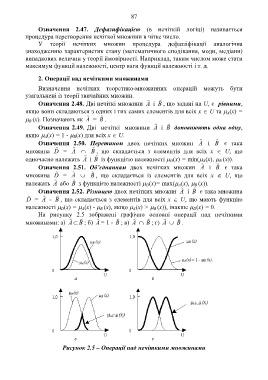
На рисунку 2.5 зображені графічно основні операції над нечіткими
множинами: а) A B ; б) A = 1 - B ; в) A B ; г) A B .
Рисунок 2.5 – Операції над нечіткими множинами