Page 86 - 4570

85




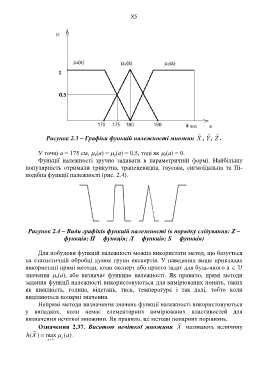
Рисунок 2.3 – Графіки функцій належності множин X , Y , Z .

У точці а = 175 см,  x(a) =  y(a) = 0,5, тоді як  z(a) = 0.
Функції належності зручно задавати в параметричній формі. Найбільшу
популярність отримали трикутна, трапецевидна, гаусова, сигмоїдальна та Пі-
подібна функції належності (рис. 2.4).

Рисунок 2.4 – Види графіків функцій належності (в порядку слідування: Z –
функція; П функція; Л функція; S функція)

Для побудови функцій належності можна використати метод, що базується
на статистичній обробці думок групи експертів. У наведених вище прикладах
використані прямі методи, коли експерт або просто задає для будь-якого а  U

значення  x(a), або визначає функцію належності. Як правило, прямі методи
задання функції належності використовуються для вимірюваних понять, таких
як швидкість, година, відстань, тиск, температура і так далі, тобто коли
виділяються полярні значення.
Непрямі методи визначення значень функції належності використовуються
у випадках, коли немає елементарних вимірюваних властивостей для
визначення нечіткої множини. Як правило, це методи попарних порівнянь.

Означення 2.37. Висотою нечіткої множини X називають величину
~
h (X )  max  (a ).
a U x