Page 44 - 4565

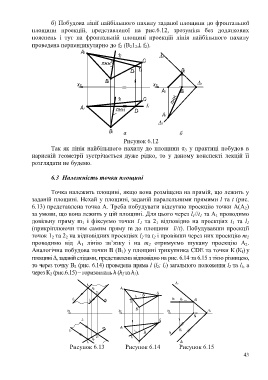
б) Побудова лінії найбільшого нахилу заданої площини до фронтальної
площини проекцій, представленої на рис.6.12, зрозуміла без додаткових
пояснень і тут на фронтальній площині проекцій лінія найбільшого нахилу
проведена перпендикулярно до f 2 (В 21 2 f 2).
A 2
1 2 2
л . н . н . C 2
f 2
D 2 B 2
B 2
x 1 2 x 1 2 х
л . н . .н
A 2 B 1
1 1 C 1
f 1
A 1 л . н . .
н
D 1
A 1
1
B 1 а б

Рисунок 6.12
Так як лінія найбільшого нахилу до площини π 3 у практиці побудов в
нарисній геометрії зустрічається дуже рідко, то у даному конспекті лекцій її
розглядати не будемо.

6.3 Належність точки площині

Точка належить площині, якщо вона розміщена на прямій, що лежить у
заданій площині. Нехай у площині, заданій паралельними прямими l та t (рис.
6.13) представлена точка А. Треба побудувати відсутню проекцію точки А(А 2)

за умови, що вона лежить у цій площині. Для цього через l 1//t 1 та А 1 проводимо
довільну пряму m 1 і фіксуємо точки 1 1 та 2 1 відповідно на проекціях t 1 та l 1
(прикріплюючи тим самим пряму m до площини l//t). Побудувавши проекції
точок 1 2 та 2 2 на відповідних проекціях l 2 та t 2 і провівши через них проекцію m 2
проводимо від А 1 лінію зв’язку і на m 2 отримуємо шукану проекцію А 2.
Аналогічна побудова точки В (В 1) у площині трикутника CDE та точки К (К 1 ) у
площині , заданій слідами, представлена відповідно на рис. 6.14 та 6.15 з тією різницею,
то через точку В 2 (рис. 6.14) проведена пряма l (l 2; l 1) загального положення l 2 та l 1, а
через К 2 (рис.6.15) – горизонталь h (h 2 та h 1).

2
1 2
А 2 A 2
2 2 C 2
B 2
l 2
t 2 h 2 K 2
l 2 m N 2
1 2
2
B 2
x 1 2 x 1 2 x 1 2 x
N 1
l 1 C 1
m 1 A 1
t 1 l 1 K 1
B 1 h 1
2 1 1 1
А 1
1 1 B 1
Рисунок 6.13 Рисунок 6.14 Рисунок 6.15
43