Page 158 - 4371

 p  p
нок 5.15). Тоді F  ,0  , рівняння директриси y   і
 2  2
 x 2  0 x  x 2 p  x 3 px
 
нехай  xA , 0  . Отже S     dx  0  0 .
 0 2 p  2p 2  6p 2
  0  

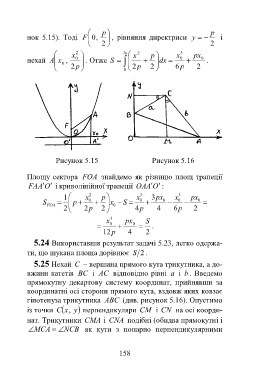
Рисунок 5.15 Рисунок 5.16

Площу сектора FOA знайдемо як різницю площ трапеції
FA A O і криволінійної трапеції OA A O :
1  x 2 p  x 3 3px x 3 px
S   p 0  x  S  0  0  0  0 
FOA   0
2  2p 2  4p 4 6p 2
x 3 px S
 0  0  .
12p 4 2
5.24 Використавши результат задачі 5.23, легко одержа-
ти, що шукана площа дорівнює S 2 .
5.25 Нехай C – вершина прямого кута трикутника, а до-
вжини катетів BC і AC відповідно рівні a і b . Введемо
прямокутну декартову систему координат, прийнявши за
координатні осі сторони прямого кута, вздовж яких ковзає
гіпотенуза трикутника ABC (див. рисунок 5.16). Опустимо
із точки xC ,  y перпендикуляри CM і CN на осі коорди-
нат. Трикутники CMA і CNA подібні (обидва прямокутні і
 MCA   NCB як кути з попарно перпендикулярними

158