Page 210 - 4196

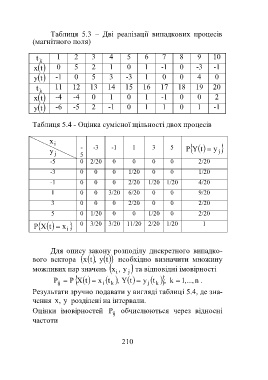
Таблиця 5.3 – Дві реалізації випадкових процесів
(магнітного поля)

t 1 2 3 4 5 6 7 8 9 10
k
x  t 0 5 2 1 0 1 -1 0 -3 -1
y  t -1 0 5 3 -3 1 0 0 4 0
t 11 12 13 14 15 16 17 18 19 20
k
x  t -4 -4 0 1 0 1 -1 0 0 2
y  t -6 -5 2 -1 0 1 1 0 1 -1

Таблиця 5.4 - Оцінка сумісної щільності двох процесів

x
i
- -3 -1 1 3 5 P Y  t  y
y 5 j 
j
-5 0 2/20 0 0 0 0 2/20
-3 0 0 0 1/20 0 0 1/20
-1 0 0 0 2/20 1/20 1/20 4/20
1 0 0 3/20 6/20 0 0 9/20
3 0 0 0 2/20 0 0 2/20
5 0 1/20 0 0 1/20 0 2/20
0 3/20 3/20 11/20 2/20 1/20 1
P X  t  x i 

Для опису закону розподілу дискретного випадко-
вого вектора     tx , y  t необхідно визначити множину
можливих пар значень  ,x i y j  та відповідні імовірності
P  P X  t  x i    tY,t k  y j   k,t k  1 ,..., n .
ij
Результати зручно подавати у вигляді таблиці 5.4, де зна-
чення ,x y розділені на інтервали.
Оцінки імовірностей P обчислюються через відносні
ij
частоти

210