Page 67 - 4169

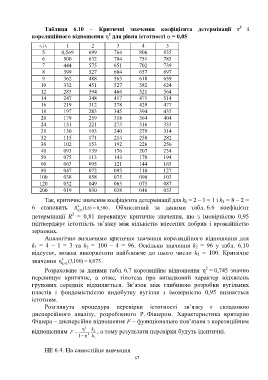
Таблиця 6.10 – Критичні значення коефіцієнта детермінації r 2 і
2
кореляційного відношення  для рівня істотності  = 0,05
k 2 k 1 2 3 4 5
1
5 0,569 699 764 806 835
6 500 632 704 751 785
7 444 575 651 702 739
8 399 527 604 657 697
9 362 488 563 618 659
10 332 451 527 582 624
12 283 394 466 521 564
14 247 348 417 471 514
16 219 312 378 429 477
18 197 283 345 394 435
20 179 259 318 364 404
24 151 221 273 316 353
28 130 193 240 279 314
32 115 171 214 250 282
36 102 153 192 226 256
40 093 139 176 207 234
50 075 113 143 170 194
60 063 095 121 144 165
80 047 072 093 110 127
100 038 058 075 090 103
120 032 049 063 075 087
200 019 030 038 046 053

Так, критичне значення коефіцієнта детермінації для k 1 = 2 – 1 = 1 і k 2 = 8 – 2 =
6 становить R 2 ) 6 , 1 (  , 0 500. Обчислений за даними табл. 6.6 коефіцієнт
, 0 95
2
детермінації R = 0,81 перевищує критичне значення, що з імовірністю 0,95
підтверджує істотність зв’язку між кількістю внесених добрив і врожайністю
зернових.
Аналогічно визначимо критичне значення кореляційного відношення для
k 1 = 4 – 1 = 3 та k 2 = 100 – 4 = 96. Оскільки значення k 2 = 96 у табл. 6.10
відсутнє, можна використати найближче до нього число k 2 = 100. Критичне
2
значення  , 3 ( 100 )  , 0 075.
, 0 95
2
Розраховане за даними табл. 6.7 кореляційне відношення  = 0,745 значно
перевищує критичне, а отже, гіпотеза про випадковий характер відхилень
групових середніх відхиляється. Зв’язок між глибиною розробки вугільних
пластів і фондомісткістю видобутку вугілля з імовірністю 0,95 визнається
істотним.
Розглянута процедура перевірки істотності зв’язку є складовою
дисперсійного аналізу, розробленого Р. Фішером. Характеристика критерію
Фішера – дисперсійне відношення F – функціонально пов’язана з кореляційним

 2 k
відношенням F  2 , а тому результати перевірки будуть ідентичні.
1  2 k 1

НЕ 6.4. На самостійне вивчення

67