Page 29 - 4168

Z = f (x 1 , x 2 ,..., x n ) → max(min) , (3.1)
при (xg 1 , x 2 ,..., x ≤ ; i ;i = , 1 k , j = , 1 ) n
) b
n
Універсального методу розв’язання нелінійних задач не
існує. Це пояснюється тим, що математична модель має мно-
жину розв’язків, яка в загальному випадку не є опуклою, або
кількість крайніх точок нескінченна. У зв’язку цим методи НП
розробляються під спеціальні класи задач.
Виділяють два класи задач НП – опукле та не опукле про-
грамування. У першому випадку розглядають опуклі цільові
функції та опуклі області допустимих розв’язків, які задають
нерівностями обмежень. Задачі опуклого програмування нази-
вають також одноекстремальними, оскільки в них існує одна
екстремальна точка, яка становить глобальний екстремум. У
другому випадку або цільова функція, або обмеження, або те й
інше не опуклі. Задачі неопуклого програмування називають
також багатоекстремальними.
У задачах електроенергетики маємо справу з нелінійним
опуклим програмуванням, для чого розроблені загальні ефек-
тивні методи.
Функція f (x ) є опукла на інтервалі a ≤ x ≤ b , якщо для
будь-яких 2-х точок x та x з цього інтервалу справедлива
1
2
нерівність:
f { x +λ 1 1 ( − λ ) x⋅ 2 }≤ λ f (x 1 ) + 1 ( − λ ) f ⋅ (x 2 ) , (3.2)
при 0 ≤ λ ≤ 1.
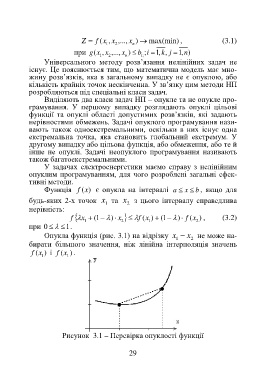
Опукла функція (рис. 3.1) на відрізку x − x не може на-
1
2
бирати більшого значення, ніж лінійна інтерполяція значень
f (x 1 ) і (xf 1 ) .

Рисунок 3.1 – Перевірка опуклості функції

29