Page 93 - 256_

 h   00 
Після підстановки початкових умов   00 h і у
вираз (3.59), маємо
kT 1   t kT 1  t
C   3 ; C   4 , (3.60)
1 2
T  T T  T
3 4 3 4

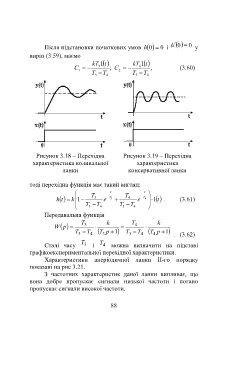
Рисунок 3.18 – Перехідна Рисунок 3.19 – Перехідна
характеристика коливальної характеристика
ланки консервативної ланки

тоді перехідна функція має такий вигляд:
 T  t T  t 
  kth   1 3 e T 3  4 e T 4   t 1  . (3.61)
 T  T T  T 
 3 4 3 4 
Передавальна функція
T k T k
W   p 3   4 
T T  pT   1 T  T T p   1
3 4 3 3 4 4 . (3.62)
T T
Сталі часу 3 і 4 можна визначити на підставі
графікоекспериментальної перехідної характеристики.
Характеристики аперіодичної ланки ІІ-го порядку
показані на рис 3.21.
З частотних характеристик даної ланки випливає, що
вона добре пропускає сигнали низької частоти і погано
пропускає сигнали високої частоти.

88