Page 90 - 256_

3.7 Інерційні ланки другого порядку

Диференціальне рівняння ланок ІІ-го порядку має вигляд
d 2 y  t dy  t
T 2  T 1  y   kxt   t
dt dt . (3.51)
Йому відповідає рівняння динаміки в операторній формі

T p 2 Y   Tp  pY   Yp   p  kX  p
2 1 (3.52)
і передавальна функція
Y   p k
W   p 
X  p T 2 p 2  T p  1
2 1 . (3.53)
T 2 p 2  T p  1  0
Характеристичне рівняння 2 1 має два
корені
 2 2 
 T T 1  4T 2 
p 1, 2     
 2T 2 2 2T 2 2 
  . (3.54)
Характер перехідного процесу залежить від типу
коренів, які можуть бути дійсними, комплексними і уявними.

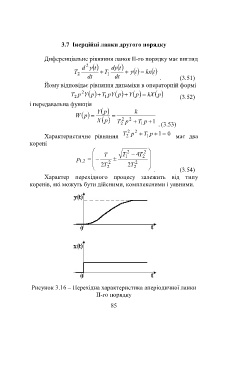
Рисунок 3.16 – Перехідна характеристика аперіодичної ланки
ІІ-го порядку

85