Page 31 - 169

k
x ,
для дискретних сигналів - I  t  i (3.3)
 i 0
   
де:  Ek   , t – крок дискретизації.
 t 

 x ) (t  x i

t i

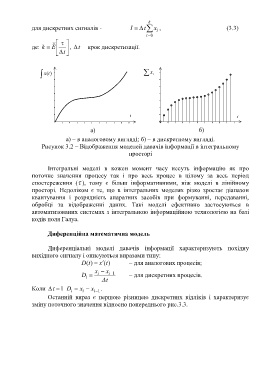
а) б)

а) – в аналоговому вигляді; б) – в дискретному вигляді.
Рисунок 3.2 – Відображення моделей давачів інформації в інтегральному
просторі

Інтегральні моделі в кожен момент часу несуть інформацію як про
поточне значення процесу так і про весь процес в цілому за весь період
спостереження ( ), тому є більш інформативними, ніж моделі в лінійному
просторі. Недоліком є те, що в інтегральних моделях різко зростає діапазон
квантування і розрядність апаратних засобів при формуванні, передаванні,
обробці та відображенні даних. Такі моделі ефективно застосуються в
автоматизованих системах з інтегральною інформаційною технологією на базі
кодів поля Галуа.

Диференційна математична модель

Диференціальні моделі давачів інформації характеризують похідну
вихідного сигналу і описуються виразами типу:
D (t )  x (t ) – для аналогових процесів;
x  x
D  i i 1 – для дискретних процесів.
i
t 
Коли t  1 D i  x i  x  i 1 .

Останній вираз є першою різницею дискретних відліків і характеризує
зміну поточного значення відносно попереднього рис.3.3.