Page 30 - 169

бути неперервним, або дискретним. Таким чином, інформаційні моделі теж
можна поділити на дві групи: аналогові і дискретні.

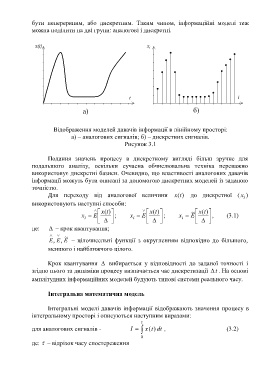
x(t) x i

t i

a) б)

Відображення моделей давачів інформації в лінійному просторі:
а) – аналогових сигналів; б) – дискретних сигналів.
Рисунок 3.1

Подання значень процесу в дискретному вигляді більш зручне для
подальшого аналізу, оскільки сучасна обчислювальна техніка переважно
використовує дискретні базиси. Очевидно, що властивості аналогових давачів
інформації можуть бути описані за допомогою дискретних моделей із заданою
точністю.
Для переходу від аналогової величини x (t ) до дискретної ( x )
i
використовують наступні способи:
  (tx  )   (tx  ) ~  (tx  )
x i  E   ; x i  E   ; x i  E   , (3.1)
        

де:  – крок квантування;
  ~
E, E, E – цілочисельні функції з округленням відповідно до більшого,
меншого і найближчого цілого.

Крок квантування  вибирається у відповідності до заданої точності і
згідно нього та динаміки процесу визначається час дискретизації t . На основі

амплітудних інформаційних моделей будують типові системи реального часу.

Інтегральна математична модель

Інтегральні моделі давачів інформації відображають значення процесу в
інтегральному просторі і описуються наступним виразами:

для аналогових сигналів - I   x (t ) dt , (3.2)

0
де:  – відрізок часу спостереження