Page 93 - 130

93

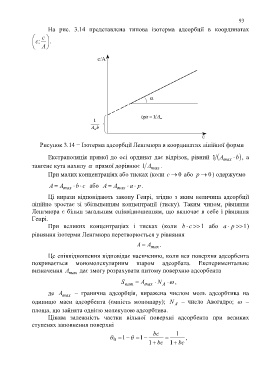
На рис. 3.14 представлена типова ізотерма адсорбції в координатах
 c 
 ;c  .
 A 

Рисунок 3.14 − Ізотерма адсорбції Ленгмюра в координатах лінійної форми

Екстраполяція прямої до осі ординат дає відрізок, рівний A1 max  b  , а
тангенс кута нахилу  прямої дорівнює A1 max .

При малих концентраціях або тисках (коли c 0 або p 0) одержуємо

A  A max b  c  або A  A max  a  p .

Ці вирази відповідають закону Генрі, згідно з яким величина адсорбції
лінійно зростає зі збільшенням концентрації (тиску). Таким чином, рівняння
Ленгмюра є більш загальним співвідношенням, що включає в себе і рівняння
Генрі.
При великих концентраціях і тисках (коли b  c  1 або a  p  1)
рівняння ізотерми Ленгмюра перетворюється у рівняння

A  A max .

Це співвідношення відповідає насиченню, коли вся поверхня адсорбента
покривається мономолекулярним шаром адсорбата. Експериментальне
визначення A max дає змогу розрахувати питому поверхню адсорбента

S пит  A max  N A   ,

де A max – гранична адсорбція, виражена числом моль адсорбтива на

одиницю маси адсорбента (ємність моношару); N – число Авогадро;  –
A
площа, що зайнята однією молекулою адсорбтива.
Цікава залежність частки вільної поверхні адсорбента при великих
ступенях заповнення поверхні

bc 1
 0 1  1   ,
1  bc 1  bc