Page 76 - 126

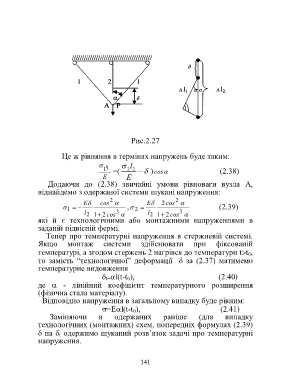
Рис.2.27

Це ж рівняння в термінах напружень буде таким:
 l 1  l
1 =( 2 2   ) cos (2.38)

E E
Додаючи до (2.38) звичайні умови рівноваги вузла А,
віднайдемо з одержаної системи шукані напруження:
2 2
E  cos  E  2cos 
   , 2  (2.39)
1
l 2 1 2cos 3  l 2 1 2cos 3 
які й є технологічними або монтажними напруженнями в
заданій підвісній фермі.
Тепер про температурні напруження в стержневій системі.
Якщо монтаж системи здійснювати при фіксованій
температурі, а згодом стержень 2 нагрівся до температури tt 0,
то замість “технологічної” деформації  за (2.37) матимемо
температурне видовження
 t=l(t-t 0), (2.40)
де  - лінійний коефіцієнт температурного розширення
(фізична стала матеріалу).
Відповідно напруження в загальному випадку буде рівним:
=El(t-t 0), (2.41)
Заміняючи в одержаних раніше (для випадку
технологічних (монтажних) схем, попередніх формулах (2.39)
 на  t одержимо шуканий розв’язок задачі про температурні
напруження.

141