Page 53 - 70

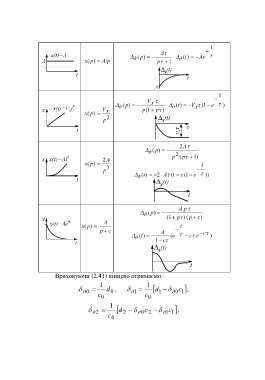
1
A   
 ( p)    t)(  Ae
д
д
x( p ) A/p  p  1

1
V x  
 д ( ) p    д (t )  V x (  1 e  )
V x ( p 1 )  p
x( p )
2
p

2 A
 д (p )   2
p ( p  ) 1
2A
x( p ) t
p 3 
 д (t )  2  A  (t  (  1  e  ))

A p 
 д (p )   (1 ( )  p p  ) 
A
x( p ) t
p  c A    c
 (t )   (e   c  e )
д 1   c

Враховуючи (2.41) кінцево отримаємо:
1 1
 д 0  d ,  1 д  d   д 0 c 1 ,
0
1
c 0 c 0
1
 д 2  d   д 0 c   1 д c 1 ,
2
2
c 0

49