Page 203 - 6624

вакуумного простору, тобто центр перерізу 1-1. Це можна
показати з допомогою рівняння Бернуллі, записаного для
перерізів 1-1 і 2-2 (рис. 6.9, а)

p  2 p  2     2
1 1 2 2 1 2 (6.33)
    .
 g 2 g  g 2 g 2 g

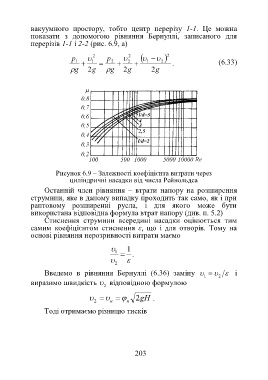
Рисунок 6.9 – Залежності коефіцієнта витрати через
циліндричні насадки від числа Рейнольдса
Останній член рівняння – втрати напору на розширення
струмини, яке в даному випадку проходить так само, як і при
раптовому розширенні русла, і для якого може бути
використана відповідна формула втрат напору (див. п. 5.2)
Стиснення струмини всередині насадки оцінюється тим
самим коефіцієнтом стиснення ε, що і для отворів. Тому на
основі рівняння нерозривності витрати маємо
 1
1
 .
 
2
Введемо в рівняння Бернуллі (6.36) заміну     і
1 2
виразимо швидкість  відповідною формулою
2
     2 gH .
2 н н
Тоді отримаємо різницю тисків

203