Page 69 - 6377

(31)
2

2
2
2
2
= 2 1 − 0 sin = 2 − sin .
2 0

З врахуванням втрати півхвилі для оптичної різниці ходу отримаємо:


2
∆= 2 − sin ± . (32)
2
2
0
2

В точці буде максимум, коли:


2
2
2
2 − sin ± = , (33)
0
2

мінімум, коли:

 
2
2
2
2 − sin ± = 2 + 1 , (34)
0
2 2

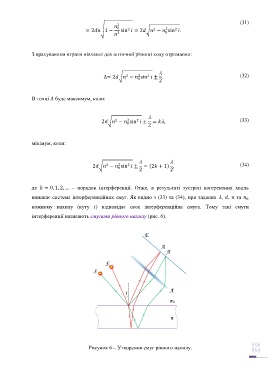
де = 0, 1, 2, … – порядок інтерференції. Отже, в результаті зустрічі когерентних хвиль
виникає система інтерференційних смуг. Як видно з (33) та (34), при заданих , , та
0
кожному нахилу (куту ) відповідає своя інтерференційна смуга. Тому такі смуги

інтерференції називають смугами рівного нахилу (рис. 6).

Рисунок 6 – Утворення смуг рівного нахилу.