Page 35 - 6101

[t 2 ]b  [t cos t ]b  [t sin t ]b  [tS ];
1 2 3
2
[t cos t ]b  [cos  t ]b  [cos t sin t ]b  [S cos ]; t (2.30)
1 2 3
2
[t sin t ]b  [cos t sin t ]b  [sin  t ]b  [S sin ]. t
1 2 3
В табл. 2.5 наведено приклад вимірювання осідань у 9 робочих циклах. Кут t синусоїди
визначається за формулою (2.28) через період коливань і задається в радіанах. Внизу таблиці
наведено поправки, сума яких наближена до нуля, що дозволяє визначити похибку одного осідання
  44 , 75 6 /  , 2 73 мм. Похибки коефіцієнтів апроксимації такі:

m  , 2 73 , 0 0022  , 0 13 мм/міс.; m  , 2 73 , 0 0000014  , 0 0033 мм/міс 2 .
1 a 2 a
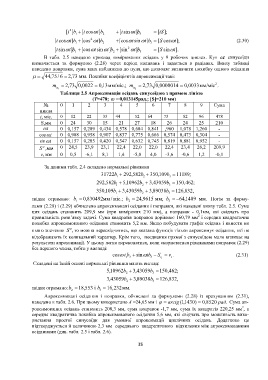
Таблиця 2.5 Апроксимація осідань синусоїдою з прямою лінією
(T=478;  0,013145рад.; [S]=210 мм)
№ 0 1 2 3 4 5 6 7 8 9 Сума
цикла
t, міс. 0 12 22 33 44 52 64 73 82 96 478
S,мм 0 24 30 15 21 27 18 26 24 25 210
t  0 0,157 0,289 0,434 0,578 0,684 0,841 ,960 1,078 1,260 -
сos t 0 0,988 0,958 0,907 0,837 0,775 0,666 0,574 0,473 0,304 -
sin t 0 0,157 0,285 0,420 0,547 0,632 0,745 0,819 0,881 0,952 -
a
S ,мм 0 24,5 23,9 23,1 22,4 22,0 22,0 22,4 23,4 26,2 209,9
v, мм 0 0,5 -6,1 8,1 1,4 -5,0 4,0 -3,6 -0,6 1,2 -0,1

За даними табл. 2.4 складено нормальні рівняння
31722 b 292 , 582 b 350 , 109b  11189 ;
1 2 3
292 , 582 b , 5 10962b  , 3 43059b  150 , 462 ;
1 2 3
350 , 109 b , 3 43059b  , 3 89038b  126 , 832 ,
1 2 3
звідки отримано: b  , 0 830492 мм / міс .; b  24 , 9615 мм ; b   64 , 1489 мм. Потім за форму-
1 2 3
лами (2.28) і (2.29) обчислено апроксимовані осідання і поправки, які наведені внизу табл. 2.5. Сума
цих осідань становить 209,9 мм (при виміряних 210 мм), а поправок - 0,1мм, які свідчать про
2
правильність розв’язку задачі. Сума квадратів поправок дорівнює 160,79 мм і середня квадратична
похибка апроксимованого осідання становить 5,2 мм. Якщо побудувати графік осідань і нанести на
a
,
нього значення S то можна пересвідчитись, що вказана функція тільки апроксимує осідання, які не
відображають їх коливальний характер. Крім того, поєднання прямої з синусоїдою мало впливає на
результати апроксимації. У цьому легко переконатися, коли скористатися рівняннями поправок (2.29)
без першого члена, тобто у вигляді:
cos b t  sin tb  S  v . (2.31)
i 2 3 t i i
Складені на їхній основі нормальні рівняння мають вигляд:
, 5 10962b  , 3 43059b  150 , 462 ;
2 3

, 3 43059b  , 3 89038b  126 , 832 ,
2 3
звідки отримано:b  18 , 553 і b  16 , 232 мм .
2 3
Апроксимовані осідання і поправки, обчислені за формулами (2.28) із врахуванням (2.31),
наведено в табл. 2.6. При цьому використано A =24,65 мм і   arctg , 1 ( 1430 )  , 0 8520 рад . Сума ап-
2
роксимованих осідань становить 208,3 мм, сума поправок -1,7 мм, сума їх квадратів 220,25 мм , а
середня квадратична похибка апроксимованого осідання 5,6 мм, які свідчать про можливість вико-
ристання простої синусоїди для умовної апроксимації циклічних осідань. Додатково це
підтверджується й величиною 2,3 мм середнього квадратичного відхилення між апроксимованими
осіданнями (див. табл. 2.5 і табл. 2.6).

35