Page 36 - 6101

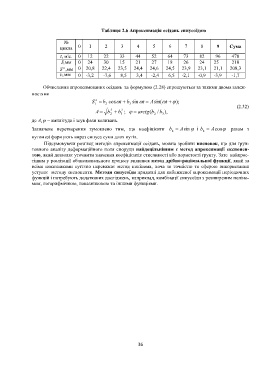
Таблиця 2.6 Апроксимація осідань синусоїдою

№
0 1 2 3 4 5 6 7 8 9 Сума
цикла
t, міс. 0 12 22 33 44 52 64 73 82 96 478
S,мм 0 24 30 15 21 27 18 26 24 25 210
S ,мм 0 20,8 22,4 23,5 24,4 24,6 24,5 23,9 23,1 21,1 208,3
a
, v мм 0 -3,2 -7,6 8,5 3,4 -2,4 6,5 -2,1 -0,9 -3,9 -1,7

Обчислення апроксимованих осідань за формулою (2.28) спрощуються за такими двома залеж-
ностями
a
S  b cos t  b sin t  A sin( t  );
t 2 3
(2.32)
2
A  b  b 2 ;   arctg (b / b ),
2 3 2 3
де ,A   амплітуда і зсув фази коливань.
Зазначене перетворення зумовлено тим, що коефіцієнти b  A sin  i b  A cos  разом з
2 2
кутом t формують вираз синуса суми двох кутів.
Підсумовуючи розгляд методів апроксимації осідань, можна зробити висновок, що для ґрун-
товного аналізу деформаційного поля споруди найдоцільнішим є метод апроксимації експонен-
тою, який дозволяє уточнити значення коефіцієнтів стисливості або пористості ґрунту. Зате найпрос-
тішим у реалізації обчислювального процесу виявився метод дрібно-раціональної функції, який за
всіма показниками суттєво переважає метод полінома, хоча за точністю та сферою використання
уступає методу експоненти. Методи синусоїди придатні для наближеної апроксимації періодичних
функцій і потребують додаткових досліджень, наприклад, комбінації синусоїди з розширеним поліно-
мом, логарифмічною, показниковою та іншими функціями.

36