Page 20 - 4849

Розв’язок. У формулі (4.7) беремо т=12, іншими словами,
відрізок ділимо на 24 частини. Обмежимося шістьма гармоніками,
нерахуючи нульової, тобто приймемо п=6. Всі обчислення для
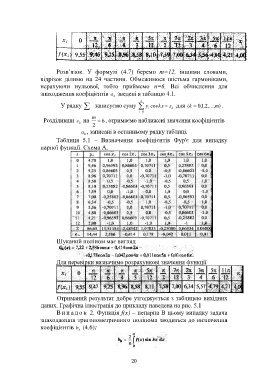
знаходження коефіцієнтів a зведені в таблицю 4.1.
k
n
У рядку  записуємо суму  y cos kx  s для (k  2 , 1 , 0 ,...,m ) .
i
k
 i 0
m
Розділивши s на  6, отримаємо наближені значення коефіцієнтів
k
2
a , записані в останньому рядку таблиці.
k
Таблиця 5.1 – Визначення коефіцієнтів Фур'є для випадку
парної функції. Схема А.

Шуканий поліном має вигляд

Для перевірки визначимо розрахункові значення функції

Отриманий результат добре узгоджується з таблицею вихідних
даних. Графічна ілюстрація до прикладу наведена на рис. 5.1
В и п а д о к 2. Функція f(x) – непарна В цьому випадку задача
знаходження тригонометричного полінома зводиться до визначення
коефіцієнтів b (4.6):
k

20