Page 66 - 4811

Infinitely Many Poles

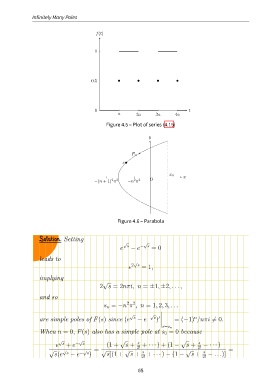
f(t)

1

0.5

0 t
a 2a 3a 4a

Figure 4.5 – Plot of series (4.15)

y

P n
s

x 0 x
2 2
2 2
−(n + 1) π −n π O

Figure 4.6 – Parabola
.

Solution. Setting
√ √
e s − e − s = 0

leads to
√
e 2 s = 1,

implying
√
2 s = 2nπi, n = ±1, ±2, . . . ,

and so
2 2
s = −n π , n = 1, 2, 3, . . .
n

√ √
n
are simple poles of F(s) since (e s − e − s ′ = (−1) /nπi ̸= 0.
)

s=s n
When n = 0, F(s) also has a simple pole at s = 0 because
0
√ √ √ √
e s + e − s (1 + s + s + · · · ) + (1 − s + s − · · · )
√ √ s − s = √ √ 2! s √ 2! s =
√
. . . . s(e − e ) s[(1 + s + 2! + · · · ) − (1 − s + 2! − . . .)]
65