Page 63 - 4811

Complex inversion formula

y

x 0 + iy n
C n

z 2 z 1
x 0 x
O
z n

x 0 − iy n

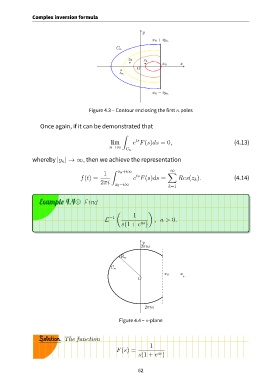
Figure 4.3 – Contour enclosing the first n poles

Once again, if it can be demonstrated that

∫
ts
lim e F(s)ds = 0, (4.13)
n→∞
C n

whereby |y | → ∞, then we achieve the representation
n
∫ x 0 +i∞ ∞
1 ∑
ts
f(t) = e F(s)ds = Res(z ). (4.14)
k
2πi x 0 −i∞
. k=1
Example 4.4, Find

( )
1
−1
L , a > 0.
as
s(1 + e )
. . . . .

y
2πni

R n

C n
x
x 0
O

−2πni

Figure 4.4 – s-plane
.

Solution. The function
1
F(s) =
as
. . . . s(1 + e )

62