Page 58 - 4811

Fourier-Mellin formula

Lemma 1 For s on C , suppose that F(s) satisfies
R
M
|F(s)| ≤ , some p > 0, all R > R .
0
|s| p
Then ∫
ts
lim e F(s)ds = 0 (t > 0).
R→∞
C R
. . . .

y
π
A( , 1)
2
1

= sin ϕ

y
0.5 2ϕ π
y =

0 ϕ
π π
6 2
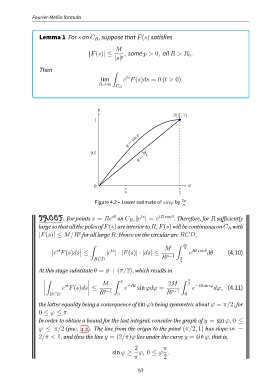
Figure 4.2 – Lower estimate of sinφ by 2φ
π

iθ
ts
PROOF. For points s = Re on C , |e | = e tR cos θ . Therefore, for R sufficiently
R
large so that all the poles of F(s) are interior to R, F(s) will be continuous on C with
R
p
|F(s)| ≤ M/R for all large R. Hence on the circular arc BCD,
∫ ∫ 3π
M 2
st ts Rt cos θ

e F(s)ds ≤ |e | · |F(s)| · |ds| ≤ p−1 e dθ. (4.10)
BCD R π
2
At this stage substitute θ = ϕ + (π/2), which results in
∫ ∫ π ∫ π
M 2M 2
st −Rt −Rt sin φ
e F(s)ds ≤
e sin φdφ = e dφ, (4.11)
R p−1 R p−1
BCD 0 0
the latter equality being a consequence of sin φ’s being symmetric about φ = π/2, for
0 ≤ φ ≤ π.
In order to obtain a bound for the last integral, consider the graph of y = sin φ, 0 ≤
φ ≤ π/2 (рис. 4.2). The line from the origin to the point (π/2, 1) has slope m =
2/π < 1, and thus the line y = (2/π)φ lies under the curve y = sin φ, that is,

2 π
sin φ ≥ φ, 0 ≤ φ .
. . . . π 2

57