Page 127 - 4776

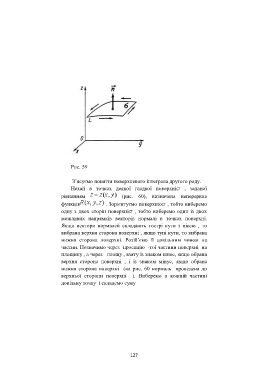
Рис. 59

З’ясуємо поняття поверхневого інтеграла другого роду.
Нехай в точках деякої гладкої поверхні , заданої
рівнянням (рис. 60), визначена неперервна
функція . Зорієнтуємо поверхню , тобто виберемо
одну з двох сторін поверхні , тобто виберемо один із двох
можливих напрямків векторів нормалі в точках поверхні.
Якщо вектори нормалей складають гострі кути з віссю , то
вибрана верхня сторона поверхні , якщо тупі кути, то вибрана
нижня сторона поверхні. Розіб’ємо її довільним чином на
частин. Позначимо через проекцію -тої частини поверхні на
площину , а через площу , взяту із знаком плюс, якщо обрана
верхня сторона поверхні , і із знаком мінус, якщо обрана
нижня сторона поверхні (на рис. 60 нормаль проведена до
верхньої сторони поверхні ). Виберемо в кожній частині
довільну точку і складемо суму

127