Page 29 - 4727

7000
6000
Витрати, грн. 4000
5000
3000
2000
1000
0
0 20 40 60 80 100 120 140 160
Машино-години

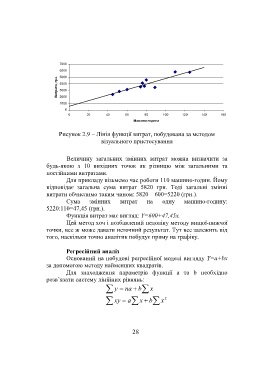
Рисунок 2.9 – Лінія функції витрат, побудована за методом
візуального пристосування

Величину загальних змінних витрат можна визначити за
будь-якою з 10 вихідних точок як різницю між загальними та
постійними витратами.
Для прикладу візьмемо час роботи 110 машино-годин. Йому
відповідає загальна сума витрат 5820 грн. Тоді загальні змінні
витрати обчислимо таким чином: 5820 – 600=5220 (грн.).
Сума змінних витрат на одну машино-годину:
5220:110=47,45 (грн.).
Функція витрат має вигляд: Y=600+47,45x.
Цей метод хоч і позбавлений недоліку методу вищої-нижчої
точки, все ж може давати неточний результат. Тут все залежить від
того, наскільки точно аналітик побудує пряму на графіку.

Регресійний аналіз
Оснований на побудові регресійної моделі вигляду Y=a+bx
за допомогою методу найменших квадратів.
Для знаходження параметрів функції а та b необхідно
розв’язати систему лінійних рівнянь:
 y  na  b  x

 xy  a  x  b  x 2

28