Page 35 - 4725

35

′
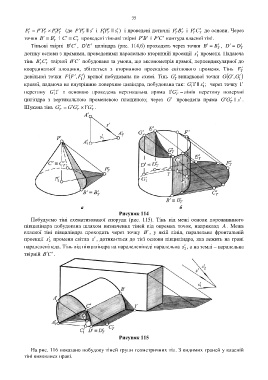
P = P ′′ P × P′ P′ (де P′ P′ || s′ і P′ P′ || s′) і проведені дотичні P′ B′ і P′ C′ до основи. Через
T
T
1
T
T
1 T
T
T
T
T
1
′
точки B ≡ B′ і C ≡ C′ проведені тіньові твірні P′ і P ′′ C контура власної тіні.
B′
′
T
T
′
′
Тіньові твірні B ′′ C , D′ E′ циліндра (рис. 114,б) проходять через точки B ≡ B′ , D ≡ D′
T
T
дотику основи з прямими, проведеними паралельно вторинній проекції s′ променя. Падаюча
1
тінь B′ T C′ твірної B ′′ C побудована за умови, що аксонометрія прямої, перпендикулярної до
T
координатної площини, збігається з вторинною проекцією світлового променя. Тінь F′
T
довільної точки ( , FFF ′ 1 ) ′ кривої побудована по схемі. Тінь G′ випадкової точки ( ,GGG ′ 1 ) ′
T
кривої, падаюча на внутрішню поверхню циліндра, побудована так: G′ 1 1′ || s′; через точку 1′
1
перетину G 1 1′ ′ з основою проведена вертикальна пряма ′G1 T ′ − лінія перетину поверхні
циліндра з вертикальною променевою площиною; через G′ проведена пряма G′ G′ || s′ .
T
Шукана тінь G = G′ G ×1 ′ G′ .
′
′
T
T
T

а б
Рисунок 114
Побудуємо тіні схематизованої споруди (рис. 115). Тінь від межі основи порожнинного
півциліндра побудована шляхом визначення тіней від окремих точок, наприклад A . Межа
власної тіні півциліндра проходить через точку B′ , у якій лінія, паралельна фронтальній
проекції s′ променя світла s′, дотикається до тієї основи півциліндра, яка лежить на грані
2
паралелепіпеда. Тінь від півциліндра на паралелепіпеді паралельна s′ , а на землі – паралельна
2
твірній B ′′ C .

Рисунок 115

На рис. 116 показано побудову тіней групи геометричних тіл. З видимих граней у власній
тіні виявилися праві.