Page 34 - 4725

34

Тінь від прямої упаде на поверхню землі (горизонтальна площина), на вертикальну стіну
α′ , на схил β ′ даху. Розв’язування виконаємо методом січних світлових площин.
Проведемо s′ і s′, які утворюють схему побудови тіні. Тінь B 1′′ T T , що впала на поверхню
1
землі від прямої A′ B′ , збігається з s′. Тінь B′ основи прямої збігається з B′ , оскільки B′
T
1
лежить на поверхні землі.
Тінь 1′ T 2′ , яка упала на стіну α′ від прямої A′ B′ , зобразиться вертикальною прямою
T
1 ′ 2 ′ || A′ B′, оскільки ′BA ′ || α′. Точка 1′ зламу тіні лежить у точці перетину α′ і s′.
T
1
T
T
Побудуємо тінь A′ . Горизонтально проекційна світлова площина Σ′ перетинає поверхні
T
3′
α′ і β ′ по ламаній 1′ T 2′ T 3′ (точку 3′ будуємо за допомогою вертикальної лінії зв’язку 3′ ,
1
′
′
яка проведена через 3 = s × a′ ). Шуканою тінню є точка ′ A T = × ′ s 1′ T 2′ T 3′.
1
1
1

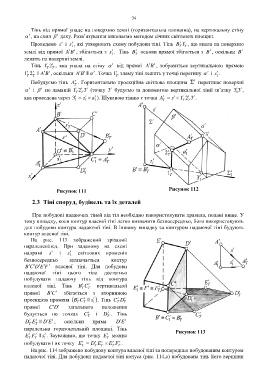
Рисунок 111 Рисунок 112

2.3 Тіні споруд, будівель та їх деталей

При побудові падаючих тіней від тіл необхідно використовувати правила, подані вище. У
тому випадку, коли контур власної тіні легко визначити безпосередньо, його використовують
для побудови контура падаючої тіні. В іншому випадку за контуром падаючої тіні будують
контур власної тіні.
На рис. 113 зображений зрізаний
паралелепіпед. При заданому на схемі
напрямі s′ і s′ світлових променів
1
безпосередньо визначається контур
B′ C′ D′ E′ F′ власної тіні. Для побудови
падаючої тіні цього тіла достатньо
побудувати падаючу тінь від контура
власної тіні. Тінь B′ T C′ вертикальної
T
прямої B′ C′ збігається з вторинною
проекцією променя (B′ T C′ T || s′ 1 ). Тінь C′ T D′
T
прямої C′ D′ загального положення
будується по точках C′ і D′ . Тінь
T
T
D′ T E′ || D′ E′ , оскільки пряма D′ E′
T

паралельна горизонтальній площині. Тінь Рисунок 113
E′ T F′ || s′ . Зауважимо, що точку E′ можна
T
T
1
побудувати і як точку E = D′ T E × E′ T F′ .
′
′
T
T
T
На рис. 114 зображено побудову контура власної тіні за попередньо побудованим контуром
падаючої тіні. Для побудови падаючої тіні конуса (рис. 114,а) побудована тінь його вершини