Page 232 - 4685

Рішення. Математично завдання формулюється у вигляді:
E14j(2 + ')4 + (13 − ')4 k;
!
[
i
K 44 + 4 ≤ 16;
!
[
24 + 24 ≤ 22;
! [
h 64 + 34 ≤ 36;
K ! [
g 4 , 4 ≥ 0 0 ≤ ' ≤ 10.
!
[
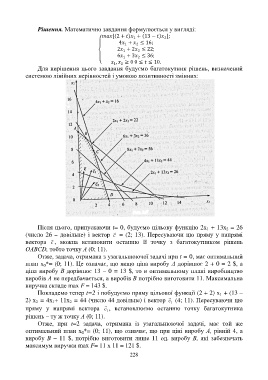
Для вирішення цього завдання будуємо багатокутник рішень, визначений
системою лінійних нерівностей і умовою позитивності змінних:

Після цього, припускаючи t= 0, будуємо цільову функцію 2x + 13х = 26
1
2
r
(число 26 – довільне) і вектор c = (2; 13). Пересуваючи цю пряму у напрямі
r
вектора c , можна встановити останню її точку з багатокутником рішень
ОАВСD, тобто точку А (0; 11).
Отже, задача, отримана з узагальнюючої задачі при t = 0, має оптимальний
план x *= (0; 11). Це означає, що якщо ціна виробу А дорівнює 2 + 0 = 2 $, а
0
ціна виробу В дорівнює 13 – 0 = 13 $, то в оптимальному плані виробництво
виробів А не передбачається, а виробів В потрібно виготовити 11. Максимальна
виручка складе max F = 143 $.
Покладемо тепер t=2 і побудуємо пряму цільової функції (2 + 2) x + (13 –
1
r
2) х = 4х + 11х = 44 (число 44 довільне) і вектор c (4; 11). Пересуваючи цю
2
1
2
1
r
пряму у напрямі вектора c , встановлюємо останню точку багатокутника
1
рішень – ту ж точку А (0; 11).
Отже, при t=2 задача, отримана із узагальнюючої задачі, має той же
оптимальний план x *= (0; 11), що означає, що при ціні виробу А, рівній 4, а
0
виробу В – 11 $, потрібно виготовити лише 11 од. виробу В, які забезпечать
максимум виручки max F= 11 х 11 = 121 $.
228