Page 66 - 4617

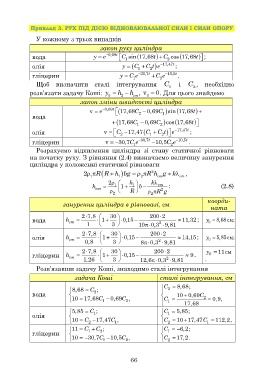
Приклад 3. РУХ ПІД ДІЄЮ ВІДНОВЛЮВАЛЬНОЇ СИЛИ І СИЛИ ОПОРУ

У кожному з трьох випадків
закон руху циліндра
 C

вода y  e  0,69t   C 1 sin 17,68t  2 cos 17,68t ;

олія y  C  Ct e  17,47t ;
1
2
гліцерин y  Ce  30,7t  C e  10,5t .
1
2
Щоб визначити сталі інтегрування C і C , необхідно
2
1
розв’язати задачу Коші: y 0  h 2 h , v 0  0. Для цього знайдемо
ст
закон зміни швидкості циліндра
v  e  0,69t  17,68C  0,69C sin 17,68t  

вода 2 1
 17,68C  1 0,69C 2 cos 17,68t 

олія v    C  2 17,47 C  1 Ct  e   17,47t ;
2 
гліцерин v   30,7Ce  30,7t  10,5C e  10,5t .
2
1
Розрахуємо відхилення циліндра зі стану статичної рівноваги
на початку руху. З рівняння (2.4) визначаємо величину занурення
циліндра у положенні статичної рівноваги

2
2 R R h bg   R h g  k ,
1 1 2 ст ст
h ст  2  1  1 h  1  b  k ст : (2.8)
 
2
2 R   Rg
2
занурення циліндра в рівновазі, см коорди-
ната

вода h ст  2 7,8     1 30    0,15  200 2   11,32; y  8,68см;
0
2

1  3  10 0,3 9,81
олія h ст  2 7,8     1 30    0,15  200 2   14,15; y  5,85см;
0

2
0,8  3  8 0,3 9,81
200 2 
y 
гліцерин h ст  2 7,8  1,26     1 30  3    0,15  12,6 0,3 9,81  9. . 0 11см
2

Розв’язавши задачу Коші, знаходимо сталі інтегрування
задача Коші сталі інтегрування, см

 8,68  C ;  C  8,68;
2


вода  2  10 0,69C

 10 17,68C  0,69C 2 ,  C  17,68 2  0,9,
1
1

 5,85  C ;  C  5,85;
олія  1  1

 10  C  17,47C 1 ,  C  2 10 17,47C  1 112,2,
2
 11  C  C ;  C   6,2;
гліцерин  1 2  1
 10   30,7C  1 10,5C 2 ,  C  17,2.
2

66