Page 154 - 4617

Приклад 7. ДИНАМІЧНИЙ ДЕМПФЕР ВИМУШЕНИХ КОЛИВАНЬ

Отже, вимушеним коливанням вагонів відповідають такі

розв’язки

  , (7.17)
x 12  4 2  28p  0,32p 2 195p 100 cos pt 22  4  28p 0,4 2 195p 100 cos pt
  ; x
2
 амплітуди вимушених коливань вагонів
Отримані закони вимушених коливань вагонів дозволяють про-
аналізувати залежність амплітуд цих коливань від частоти pзбу-
рювальної сили Q (рис. 7.4, рис. 7.5)

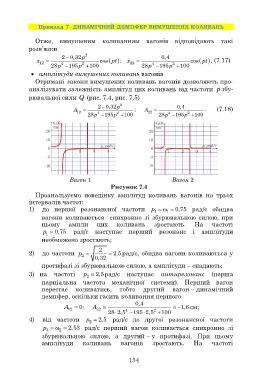
A 12  4 2  28p  0,32p 2 195p 100 ; A 22  4  28p 0,4 2 195p 100 . (7.18)
2

Вагон 1 Вагон 2
Рисунок 7.4

Проаналізуємо поведінку амплітуд коливань вагонів на трьох
інтервалів частот:
1) до першої резонансної частоти p 1   0,75 рад/с обидва

1
вагони коливаються синхронно зі збурювальною силою, при
цьому ампли цих коливань зростають. На частоті
p  0,75 рад/с наступає перший резонанс і амплітуди
1
необмежено зростають;

2) до частоти p  2  2,5рад/с, обидва вагони коливаються у
2
0,32
протифазі зі збурювальною силою, а амплітуди – спадають;
3) на частоті p 2  2,5рад/с наступає антирезонанс (перша
парціальна частота механічної системи). Перший вагон
перестає коливатись, тобто другий вагон – динамічний
демпфер, оскільки гасить коливання першого

A  0; A  0,4  1,6см;
12 22 4 2
 28 2,5  195 2,5  100
4) від частоти p 2  2,5 рад/с до другої резонансної частоти

p 3   2,53 рад/с перший вагон коливається синхронно зі

2
збурювальною силою, а другий – у протифазі. При цьому
амплітуди коливань вагонів зростають. На частоті

154