Page 103 - 4617

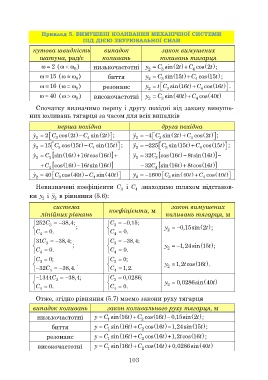
Приклад 5. ВИМУШЕНІ КОЛИВАННЯ МЕХАНІЧНОЇ СИСТЕМИ
ПІД ДІЄЮ ЗБУРЮВАЛЬНОЇ СИЛИ

кутова швидкість випадок закон вимушених
шатуна, рад/с коливань коливань тягарця
 2 (  ) низькочастотні y  C 3 sin 2t 4 cos 2t
  C
  ;
0
2

 15 (  ) биття y  C 3 sin 15t  C 4 cos 15t ;
0
2
 16 (  ) резонанс y  tC 3 sin 16t  C 4 cos 16t   .



0
2
 40 (  ) високочастотні y  C 3 sin 40t  C 4 cos 40t 
0
2
Спочатку визначимо першу і другу похідні від закону вимуше-
них коливань тягарця за часом для всіх випадків
перша похідна друга похідна
 
  C
 
  C
y  2 C cos 2t sin 2t ; y   4 C sin 2t cos 2t ;






2 3 4 2 3 4
y  15 C cos 15t  C sin 15t   ; y   225 C sin 15t  C cos 15t   ;






2 3 4 2 3 4
y  C sin 16t  16 cos 16t  t   y  32C cos 16t  8 sin 16t  t  
2 3 2 3
 C 4 cos 16t  16 sin 16t  t   32C 4 sin 16t  8 cos 16t  t 

y  40 C 3 cos 40t  C 4 sin 40t    y  2  1600 C 3 sin 40t  C 4 cos 40t   



2

Невизначені коефіцієнти C і C знаходимо шляхом підстанов-
3
4
ки y і y в рівняння (5.6):
2
2
система закон вимушених
лінійних рівнянь коефіцієнти, м коливань тягарця, м
 252C   38,4;  C   0,15;
 
 3 ;  3 y   0,15sin 2t ;
2
 C  0.  C  0.
4
4
 31C   38,4;  C   38,4;

 3 ;  3 y   1,24sin 15t ;
 C  0.  C  0. 2
4
4
 C  0;  C  0;

 3 .  3 y  1,2 cost 16t .
2
  32C  4  38,4.  C  1,2.
4
  1344C   38,4;  C  0,0286;
 3  3 y  0,0286sin 40t 
 C  0.  C  0. 2
4
4
Отже, згідно рівняння (5.7) маємо закони руху тягарця
випадок коливань закон коливального руху тягарця, м
низькочастотні y C 1 sin 16t  C 2 cos 16t  0,15sin 2t   ;
биття y C 1 sin 16t  C 2 cos 16t  1,24sin 15t   ;

резонанс y C 1 sin 16t  C 2 cos 16t  1,2 cos 16t  t ;
високочастотні y C 1 sin 16t  C 2 cos 16t  0,0286sin 40t  
103