Page 18 - 4570

17

Приклад 1.22. Точка М у прямокутній декартовій системі координат на
площині задається впорядкованою парою дійсних чисел у такий спосіб: M(x, y)
(x  R, y  R). Тоді (x, y)  R 2 = R  R. Звідси й назва добутку − декартів.
Приклад 1.23. Якщо A ={a, b, Δ, □}; B = {1, m}, то декартів добуток
матиме вигляд:
A  B = {(a, 1), (a, m), (b, 1), (b, m), (Δ, 1), (Δ, m), (□, 1), (□, m)}.
Визначимо A  B, як пари елементів по одному з кожної множини А та В
(пари елементів, що належать до декартова добутку, позначимо в таблиці
точками):

В даному випадку кожна підмножина R множини A  B є бінарним
відношенням.

Приклади 1.24:
1) Позначимо в таблиці точками елементи, які належать до підмножини R
= {(a, 1), (b, m), (Δ, □)} декартового добутку множин A та B (R  (A  B)):

Тоді R − бінарне відношення між множинами A та B.
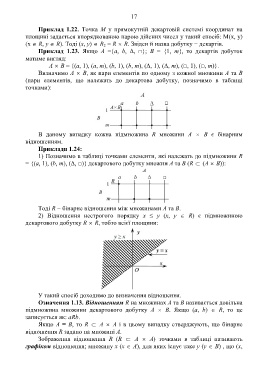
2) Відношення нестрогого порядку x ≤ y (x, y  R) є підмножиною
декартового добутку R  R, тобто всієї площини:

У такий спосіб доходимо до визначення відношення.
Означення 1.13. Відношенням R на множинах A та B називається довільна
підмножина множини декартового добутку A  B. Якщо (a, b)  R, то це
записується як: aRb.
Якщо A = B, то R  A  A і в цьому випадку стверджують, що бінарне
відношення R задано на множині A.
Зображення відношення R (R  A  A) точками в таблиці називають
графіком відношення; множину х (x  A), для яких існує таке у (y  B) , що (x,