Page 63 - 4523

цього збурення в системі в кожен момент часу буде виникати
сигнал помилки  t  x н  t , який так само буде випадковим

сигналом з нормальним розподіленням, причому сигнал
помилки теж може бути у вигляді суми двох складових
 t  m    t . (1.100)

Припускаючи, що нелінійний елемент  xf н замінений

статичною еквівалентною ланкою з двома каналами k і k
0
1
(див. рис. 11.19), можна по-різному записати вирази для двох
складових сигналу помилки
W  p
m    mp  q  p п , (1.101)
1  k o W u   p

  W  p
  p  q   p u . (1.102)
1 k 1 W u   p

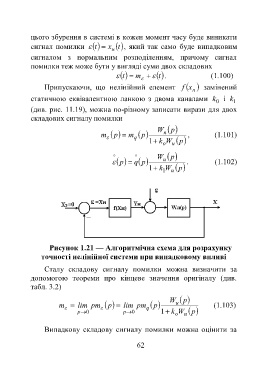
Рисунок 1.21 — Алгоритмічна схема для розрахунку
точності нелінійної системи при випадковому впливі
Сталу складову сигналу помилки можна визначити за
допомогою теореми про кінцеве значення оригіналу (див.
табл. 3.2)
W  p
m  lim pm   p  lim pm q  p u (1.103)

p0 p0 1  k o W u   p

Випадкову складову сигналу помилки можна оцінити за

62