Page 67 - 4498

increase in the potential energy of the interaction of molecules (since the
distances between them increase) at the expense of kinetic energy. As a
result, the thermal motion of the molecules slows down, and the
temperature of the expanding gas will decrease. In reality, the processes

leading to the Joule-Thomson effect are more complex, since the gas is not
isolated with respect to energy from the external medium. It does external
work (the successive portions of gas, to the right of the throttle, compress

the previous ones), and to the left of the throttle the forces of external
pressure work on the gas (maintaining the steady flow). This is taken into
account when drawing up the energy balance in the Joule-Thomson
experiments. The work of pushing through the throttle a portion of gas

occupying volume V before the throttle is p V . The same portion of gas
1 l
l
occupying volume V after the throttle does work p V . The resulting
2 2
2
external work A = p V - p V done on the gas can be either positive or
2 2
l l
negative. Under adiabatic conditions it can lead only to a change in the
internal energy of the gas: A = U - U .
2
2
Thus, ΔT can be found knowing the
equation of state of a gas and the
expression for U.
The value and sign of the Joule-

Thomson effect are determined by the
ratio of the work of the gas to the work
of the forces of external pressure as well
as by the properties of the gas itself, in

particular by the size of the molecules.
In the case of an ideal gas whose
molecules are regarded as noninteracting

material points, the Joule-Thomson
effect is equal to zero. Depending on the
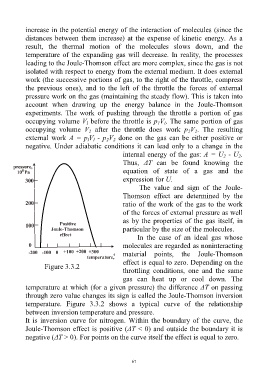
Figure 3.3.2
throttling conditions, one and the same
gas can heat up or cool down. The

temperature at which (for a given pressure) the difference ΔT on passing
through zero value changes its sign is called the Joule-Thomson inversion
temperature. Figure 3.3.2 shows a typical curve of the relationship

between inversion temperature and pressure.
It is inversion curve for nitrogen. Within the boundary of the curve, the
Joule-Thomson effect is positive (ΔT < 0) and outside the boundary it is

negative (ΔT > 0). For points on the curve itself the effect is equal to zero.

67